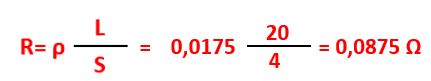REALIZZARE UN IMPIANTO FOTOVOLTAICO IN ISOLA CON INVERTER IBRIDO O CON REGOLATORE DI CARICA (CARTACEO)
(NUOVA EDIZIONE)
Lo potete scaricare gratuitamente acquistando il manuale “Progettare un impianto fotovoltaico in parallelo con la linea elettrica”.
PROGETTARE UN IMPIANTO FOTOVOLTAICO IN PARALLELO CON LA RETE ELETTRICA
PROGETTARE PICCOLI IMPIANTI FOTOVOLTAICI IN FORMATO CARTACEO
RESISTIVITA’ ELETTRICA
La resistività elettrica, anche detta resistenza elettrica , è una grandezza fisica che varia a seconda dei materiali e della geometria di un corpo, e indica una resistenza specifica, ovvero la resistenza per una unità di lunghezza e di sezione.
La resistività viene espressa matematicamente nella seconda legge di ohm che si scrive:
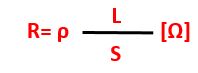
La resistività differisce dalla resistenza in quanto è una proprietà specifica del materiale e dipende principalmente dalla struttura microscopica del mezzo; al contrario la resistenza R è una proprietà dell’intero conduttore in esame (proprietà macroscopica).
La seconda legge di Ohm rappresenta quindi un metodo di calcolo di una resistenza partendo dalle qualità costruttive di un materiale, dove:
R= resistività elettrica (Ω); ρ= resistività del materiale (Ω*m); L= lunghezza del materiale (m); S= sezione del materiale (m²).
I parametri in questo caso non variano nel tempo, ma sono fissi.
La seconda legge di Ohm ci dice quindi che la resistenza di un corpo è direttamente proporzionale alla resistività (che dipende a sua volta dal materiale e, in misura minore, dalla temperatura) e alla lunghezza e inversamente proporzionale alla sezione.
Fino ad ora si è usata la relazione con risposta R, ma la formula può essere scritta matematicamente anche nei seguenti modi:
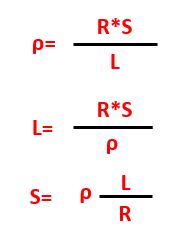
Se consideriamo la prima formula di queste tre si può dedurre che la resistività “ρ” si misuri in “Ω*m” in quanto “R” si misura in “Ω“, la “S” in “m²” e “L” in “m” quindi “Ω*m²/m“, semplificando si ottiene “Ω*m“.
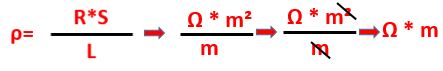
Ma le misure espresse in tale unità risultano tuttavia piuttosto piccole per i normali materiali conduttori (esempio il rame), per cui nella pratica molto spesso si usa come unità di misura l’ohm per mm2 (Ω*mm²) di sezione, e il metro di lunghezza (Ω∙mm2/m), equivalente al μΩ∙m, cioè a 10–6 Ω∙m.
La resistività di un metallo aumenta all’aumentare della temperatura:
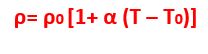
Dove: ρ= è la resistività e T è la temperatura, ρo= è la resistività del metallo alla temperatura T0 di riferimento, solitamente 20 °C, α= è il coefficiente termico dipendente dal materiale.
La resistività ρ del rame alla temperatura di 20 °C, è:
ρ20 =0,0175 Ω∙mm2/m
e il coefficiente termico (α) sempre a 20°C, è:
α20= 3,95 * 10¯³ = 0,00395
Per trovare la resistività ρ alla temperatura t:
ρt = ρ20 [1+ α(T-T20)]
Dove: ρt = resistività alla temperatura indicata; ρ20= resistività alla temperatura convenzionale (20 °C= 0,0175 Ω∙mm2/m); α= coefficiente termico e dipende dal materiale (rame a 20°C= 3,95*10¯³ = 0,00395); T-T20 = T è la temperatura a cui si vuole calcolare la resistività in °C, T20 temperatura di riferimento :20 °C.
Esempio: voglio calcolare la resistività a 70°C di un cavo in rame rispetto a quella di riferimento di 20°C.
ρt = ρ20 [1+ α(T-T20)]= 0,0175[1+0,00395(70-20)]= 0,021 Ω∙mm2/m
Alcuni valori del ρ del rame rispetto alle varie temperature:
ρ20 = 0,0175 Ω∙mm2/m; ρ30= 0,018 Ω∙mm2/m; ρ60= 0,02 Ω∙mm2/m; ρ70= 0,021 Ω∙mm2/m.
Se il coefficiente termico α è negativo la resistività diminuisce, per cui al diminuire della temperatura la resistività diminuisce e aumenta all’aumentare della temperatura e di conseguenza anche la resistenza elettrica.
Se volessimo calcolare la resistenza elettrica di un cavo in rame lungo 20 m, e con una sezione di 4 mm², alla temperatura di 20°C con un ρ20 = 0,0175 Ω∙mm2/m il valore è:
