VITO SPERONI CONSULENTE SULLE TELECOMUNICAZIONI E FOTOVOLTAICO

LEGGE DI Ohm (CORRENTE CONTINUA)
A temperatura costante, la differenza di potenziale (V) applicata a due estremità di un conduttore metallico è direttamente proporzionale all’intensità della corrente (I) che percorre il conduttore.
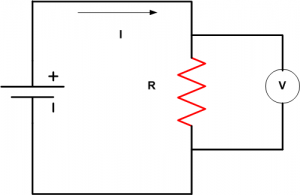
Per la legge di Ohm, se R è la resistenza del conduttore, V è la differenza di potenziale agli estremi della resistenza e I è l’intensità della corrente: valgono le seguenti relazioni.
V=R*I (il risultato è in Volt)
R=V/I (il risultato è in Ohm)
I=V/R (il risultato è in Ampere)
P=V*I (il risultato è in Watt, dove P è la Potenza)
TABELLA RIASSUNTIVA
P =POTENZA (Watt)
P= V x I (W) se sostituisco la V con R x I avremo che P= R x I² se sostituisco nella formula la I con V/R si avrà che P= V²/R
V= TENSIONE (Volt)
V= R x I (Volt) se sostituisco la I con P/V avremmo V²= R x P = ![]()
Se sostituisco nella formula la R con V/I avremo che V= V/I x I = P/I in quanto P= V x I
R= RESISTENZA (OHM = Ω)
R = V/I se sostituisco la V con P/I avremo che la R= P/ I² se invece sostituisco la I con P/V avremo che R= V/P/V e infine R= V²/P
I= CORRENTE (Ampere)
I= V/R se sostituisco la R con V/I avremo V/V/I e siccome V x I = P avremo che la I= P/V; se sostituisco nella formula I=P/V la V con R x I avremo che: I²= P/R per cui :
RESISTIVITA’ ELETTRICA
La resistività elettrica, anche detta resistenza elettrica , è una grandezza fisica che varia a seconda dei materiali e della geometria di un corpo, e indica una resistenza specifica, ovvero la resistenza per una unità di lunghezza e di sezione.
La resistività viene espressa matematicamente nella seconda legge di ohm che si scrive:
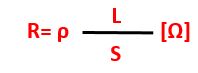
La resistività differisce dalla resistenza in quanto è una proprietà specifica del materiale e dipende principalmente dalla struttura microscopica del mezzo; al contrario la resistenza R è una proprietà dell’intero conduttore in esame (proprietà macroscopica).
La seconda legge di Ohm rappresenta quindi un metodo di calcolo di una resistenza partendo dalle qualità costruttive di un materiale, dove:
R= resistività elettrica (Ω); ρ= resistività del materiale (Ω*m); L= lunghezza del materiale (m); S= sezione del materiale (m²).
I parametri in questo caso non variano nel tempo, ma sono fissi.
La seconda legge di Ohm ci dice quindi che la resistenza di un corpo è direttamente proporzionale alla resistività (che dipende a sua volta dal materiale e, in misura minore, dalla temperatura) e alla lunghezza e inversamente proporzionale alla sezione.
Fino ad ora si è usata la relazione con risposta R, ma la formula può essere scritta matematicamente anche nei seguenti modi:
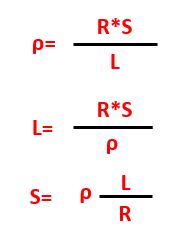
Se consideriamo la prima formula di queste tre si può dedurre che la resistività “ρ” si misuri in “Ω*m” in quanto “R” si misura in “Ω“, la “S” in “m²” e “L” in “m” quindi “Ω*m²/m“, semplificando si ottiene “Ω*m“.
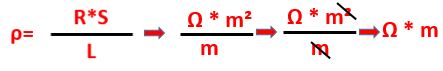
Ma le misure espresse in tale unità risultano tuttavia piuttosto piccole per i normali materiali conduttori (esempio il rame), per cui nella pratica molto spesso si usa come unità di misura l’ohm per mm2 (Ω*mm²) di sezione, e il metro di lunghezza (Ω∙mm2/m), equivalente al μΩ∙m, cioè a 10–6 Ω∙m.
La resistività di un metallo aumenta all’aumentare della temperatura:
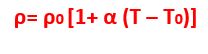
Dove: ρ= è la resistività e T è la temperatura, ρo= è la resistività del metallo alla temperatura T0 di riferimento, solitamente 20 °C, α= è il coefficiente termico dipendente dal materiale.
La resistività ρ del rame alla temperatura di 20 °C, è:
ρ20 =0,0175 Ω∙mm2/m
e il coefficiente termico (α) sempre a 20°C, è:
α20= 3,95 * 10¯³ = 0,00395
Per trovare la resistività ρ alla temperatura t:
ρt = ρ20 [1+ α(T-T20)]
Dove: ρt = resistività alla temperatura indicata; ρ0= resistività alla temperatura convenzionale (20 °C= 0,0175 Ω∙mm2/m); α= coefficiente termico e dipende dal materiale (rame a 20°C= 3,95*10¯³ = 0,00395); T-T0 = T è la temperatura a cui si vuole calcolare la resistività in °C, T20 temperatura di riferimento :20 °C.
Esempio: voglio calcolare la resistività a 70°C di un cavo in rame rispetto a quella di riferimento di 20°C.
ρt = ρ20 [1+ α(T-T20)]= 0,0175[1+0,00395(70-20)]= 0,021 Ω∙mm2/m
Alcuni valori del ρ del rame rispetto alle varie temperature:
ρ20 = 0,0175 Ω∙mm2/m; ρ30= 0,018 Ω∙mm2/m; ρ60= 0,02 Ω∙mm2/m; ρ70= 0,021 Ω∙mm2/m.
Se il coefficiente termico α è negativo la resistività diminuisce, per cui al diminuire della temperatura la resistività diminuisce e aumenta all’aumentare della temperatura e di conseguenza anche la resistenza elettrica.
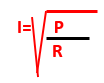
Se volessimo calcolare la resistenza elettrica di un cavo in rame lungo 20 m, e con una sezione di 4 mm², alla temperatura di 20°C con un ρ20 = 0,0175 Ω∙mm2/m il valore è: